
What is Asymptotic Notation?
Whenever we want to perform analysis of an algorithm, we need to calculate the complexity of that algorithm. But when we calculate the complexity of an algorithm it does not provide the exact amount of resource required. So instead of taking the exact amount of resource, we represent that complexity in a general form (Notation) which produces the basic nature of that algorithm. We use that general form (Notation) for analysis process.
Asymptotic notation of an algorithm is a mathematical representation of its complexity.
Note - In asymptotic notation, when we want to represent the complexity of an algorithm, we use only the most significant terms in the complexity of that algorithm and ignore least significant terms in the complexity of that algorithm (Here complexity can be Space Complexity or Time Complexity).
For example, consider the following time complexities of two algorithms…
- Algorithm 1 : $5n^2 + 2n + 1$
- Algorithm 2 : $10n^2 + 8n + 3$
Generally, when we analyze an algorithm, we consider the time complexity for larger values of input data (i.e. ‘n’ value). In above two time complexities, for larger value of ‘n’ the term ‘$2n + 1$’ in algorithm 1 has least significance than the term ‘$5n^2$’, and the term $‘8n + 3’$ in algorithm 2 has least significance than the term ‘$10n^2$’. Here, for larger value of ‘n’ the value of most significant terms ( $5n^2$ and $10n^2$ ) is very larger than the value of least significant terms ( $2n + 1$ and $8n + 3$ ). So for larger value of ‘n’ we ignore the least significant terms to represent overall time required by an algorithm. In asymptotic notation, we use only the most significant terms to represent the time complexity of an algorithm.
Majorly, we use THREE types of Asymptotic Notations and those are as follows…
- Big - Oh (O)
- Big - Omega (Ω)
- Big - Theta (Θ)
Big - Oh Notation (O)
Big - Oh notation is used to define the upper bound of an algorithm in terms of Time Complexity. That means Big - Oh notation always indicates the maximum time required by an algorithm for all input values. That means Big - Oh notation describes the worst case of an algorithm time complexity. Big - Oh Notation can be defined as follows…
Consider function f(n) as time complexity of an algorithm and g(n) is the most significant term. If $f(n) <= C g(n)$ for all $n >= n_0$, $C > 0$ and ${n}_0 >= 1$. Then we can represent f(n) as O(g(n)).
$f(n) = O(g(n))$
Consider the following graph drawn for the values of f(n) and C g(n) for input (n) value on X-Axis and time required is on Y-Axis
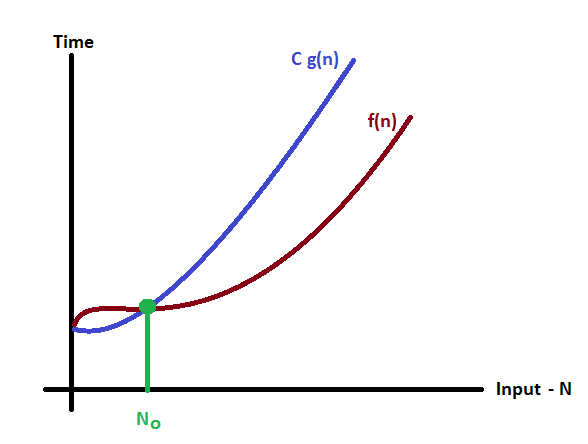
In above graph after a particular input value n0, always C g(n) is greater than f(n) which indicates the algorithm’s upper bound.
Example
Consider the following $f(n)$ and $g(n)$…
$f(n) = 3n + 2$
$g(n) = n$
If we want to represent $f(n)$ as $O(g(n))$ then it must satisfy $f(n) <= C g(n)$ for all values of $C > 0$ and ${n}_0 >= 1$
$f(n) <= C g(n)$
$⇒3n + 2 <= C n$
Above condition is always TRUE for all values of $C = 4$ and $n >= 2$. By using Big - Oh notation we can represent the time complexity as follows… $3n + 2 = O(n)$
Big - Omege Notation (Ω)
Big - Omega notation is used to define the lower bound of an algorithm in terms of Time Complexity. That means Big-Omega notation always indicates the minimum time required by an algorithm for all input values. That means Big-Omega notation describes the best case of an algorithm time complexity. Big - Omega Notation can be defined as follows…
Consider function f(n) as time complexity of an algorithm and g(n) is the most significant term. If $f(n) >= C g(n)$ for all $n >= n_0$, $C > 0$ and $n0 >= 1$. Then we can represent $f(n)$ as $Ω(g(n))$.
$f(n) = Ω(g(n))$
Consider the following graph drawn for the values of f(n) and C g(n) for input (n) value on X-Axis and time required is on Y-Axis.
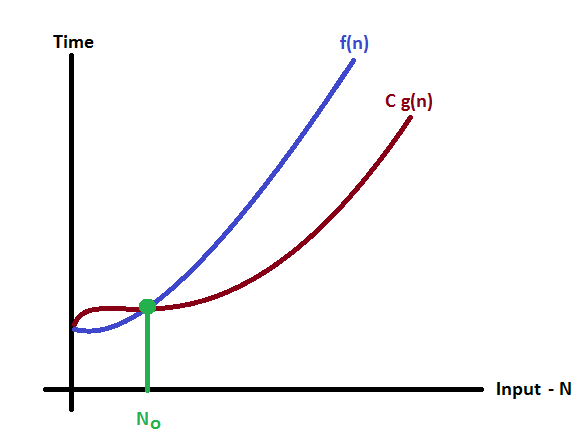
In above graph after a particular input value n0, always C g(n) is less than f(n) which indicates the algorithm’s lower bound.
Example
Consider the following f(n) and g(n)…
$f(n) = 3n + 2$ $g(n) = n$
If we want to represent f(n) as Ω(g(n)) then it must satisfy f(n) >= C g(n) for all values of C > 0 and n0>= 1 f(n) >= C g(n) ⇒3n + 2 >= C n Above condition is always TRUE for all values of C = 1 and n >= 1. By using Big - Omega notation we can represent the time complexity as follows… 3n + 2 = Ω(n)
Big - Theta Notation (Θ)
Big - Theta notation is used to define the average bound of an algorithm in terms of Time Complexity. That means Big - Theta notation always indicates the average time required by an algorithm for all input values. That means Big - Theta notation describes the average case of an algorithm time complexity. Big - Theta Notation can be defined as follows…
Consider function f(n) as time complexity of an algorithm and g(n) is the most significant term. If $C1 g(n) <= f(n) <= C2 g(n)$ for all $n >= n_0$, $C1 > 0$, $C2 > 0$ and $n_0 >= 1$. Then we can represent f(n) as $Θ(g(n))$.
$f(n) = Θ(g(n))$
Consider the following graph drawn for the values of f(n) and C g(n) for input (n) value on X-Axis and time required is on Y-Axis
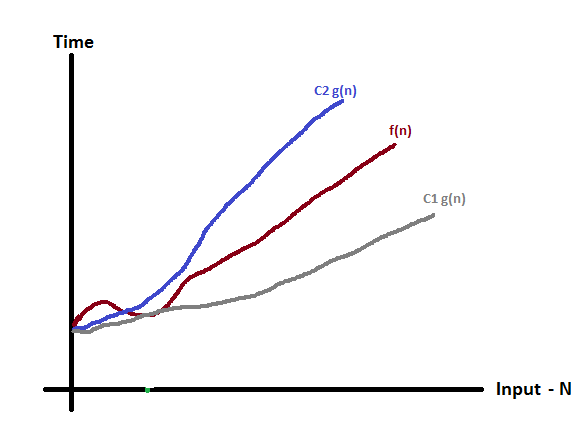
In above graph after a particular input value n0, always C1 g(n) is less than f(n) and C2 g(n) is greater than f(n) which indicates the algorithm’s average bound.
Example
Consider the following f(n) and g(n)…
$f(n) = 3n + 2$ $g(n) = n$
If we want to represent f(n) as Θ(g(n)) then it must satisfy $C1 g(n) <= f(n) <= C2 g(n)$ for all values of $C1 > 0$, $C2 > 0$ and $n_0>= 1$
$C1 g(n) <= f(n) <= C2 g(n)$ $⇒C1 n <= 3n + 2 <= C2 n$
Above condition is always TRUE for all values of C1 = 1, C2 = 4 and n >= 2. By using Big - Theta notation we can represent the time compexity as follows…
$3n + 2 = Θ(n)$